Today I’m returning to a question that’s nagged at me for about fifty years. You might call it the question of recurrence.

Would an infinite universe necessarily contain identical copies of me?

My post today uses some of the material that I wrote for the preface of the 2004 edition of my nonfiction book, Infinity and the Mind.

As is usual for my blog posts, most of images I include will have nothing to do with the text. At least not at the conscious or deliberate level. At the intuitive and synchronistic level, of course, each of them is a sly commentary and a perfect fit.

I’m thinking about the issue of recurrence again because I’m reading Max Tegmark’s stimulating 2014 book, Our Mathematical Universe. It’s has the best (only?) explanation I’ve ever seen of how cosmic inflation can be viewed as impling that the space of our universe is infinite—this is a connection I’ve always wondered about. The latter part of the book gets into the more familiar ideas that quantum mechanics might lead to an Evertt style multiverse, and to the very shaky idea that the world “is” a mathematical object, and that every mathematical object “is” an existing physical universe—which is, in the humble opiion of this mathematician, bullshit. You can find an early survey of TEgmark’s ideas in his 2003 article by Tegmark, “Parallel Universes,” in Scientific American.

Anyway, as I say, Tegmark is great on infinite space. Right off the bat, let me point out that there’s no mathematical certainty that a supertraveler across endless space with endless galaxies would necessarily find another Earth just like the one right here. Consider for instance an infinite set of integers which has only one odd member, the number 3. Someone who starts at 3 and looks for another odd number is going to be disappointed.

{2, 3, 4, 6, 8, 10, 12, … , 2n, …}

So, as a mathematician, I’ve always bridled at the physicists’ claim that an endless world has to repeat. An infinite set doesn’t have to exhaustive.

As a higher-order rebuttal to the tedious insistence that an infinite world must repeat, I’d also point out that it might be that the objects in our world are in fact infinitely complex—and are not like the Lego-style pixel-by-pixel structures that physicists like to image them to be. If matter is endlessly smooth, then there’s room for endless, non-repeating variety.

But let’s look at Tegmark’s reasoning before I argue about it any more. The thing to keep in mind is that nowadays many cosmologists believe that our space really is truly infinite, with an endless number of stars and planets. The initial Big Bang singularity is to have happened not at any single point, but across an infinite space.

Click for a larger version.

If the old image of the Big Bang was like a white dot appearing in a plane, the new image is like an entire endless plane becoming suddenly illuminated in every part. You might visualize a sheet of light settling down upon the plane.

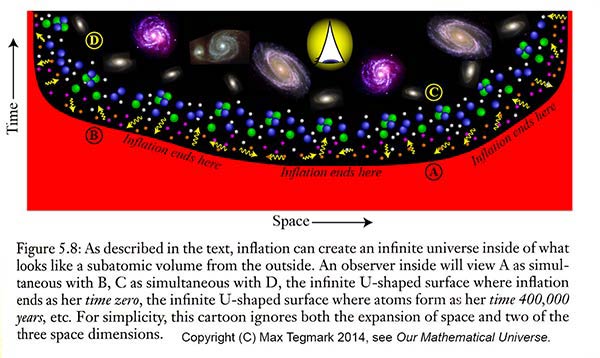
More precisely, Tegmark describes a sequence of events before the big bang: a tiny bit of darkly energetic supermatter undergoes an insanely rapid inflation which will last forever. The inflation fills out a finitely wide region of space and an infinite amount of future time. And what we perceive to be the big bang is a long, skinny, infinitely extended U-shaped hypersurface within the inflationary zone.

Click for a larger version.

Very hard to wrap your mind around this, but Tegmark gives a good presentation of the idea in Our Mathematical Universe, using the figure shown above — which is © Max Tegmark, 2014.

So what we call the Big Bang is that bumpy U-shaped line between the light (inflationary) zone and the dark (normal space) zone. And from our perspective that line is one simultaneous moment that happened fourteen billion years ago. And it’s infinitely large.

This idea is so novel, startling, and hard to understand that I’ll go over it again in my folow up post, “Against Recurrence #3“, that is in the post after next.

I’m going to have to talk about some very large finite numbers now. And the way we do that is with exponents. But it’s hard to show an exponent in HTML. So instead we’ll use a caret symbol, like ^, to mean “to the.” That is, we can think of 100 as 10^2, and 1,000,000 as being 10^6. Fine. And now we’re going to go crazy with this.

The region of our endless space that’s presently visible to us is a sphere with a diameter of some 10^27 or one octillion meters. (I should mention that the standard name for a number of the form 10^((k+1)∙3) has the general form k-illion.) This octillion-meter-wide sphere, which we can call our home volume, contains those objects that are close enough so that light from them has had time since the Big Bang moment to travel to us.

Suppose we make the unexceptionable assumption that our home volume has an average temperature of less than a hundred million degrees centigrade (the sun’s surface is a mere five thousand degrees centigrade). In this case, according to Tegmark, the home volume has room for some 10^118 protons. To get a handle on this number it’s useful to use the number googol, which is written as a one followed by a hundred zeroes, that is, a googol is 10^100.

10^118 = 10^(18 + 100) = 10^18 x 10^100 = 10^((5+1)∙3) x 10^100 = quintillion googol.

Now we can wonder how many distinct possible home-volume-sized regions there could be. Okay, this is where Tegmark and his camp “beg the question,” that is, this is where they slip in the conclusion that the want to reach, importing their eventual conclusion as a plausible observation about the state of affairs.

Here it is: “We can think of the home volume as a jungle-gym grid with a quintillion googol slots. One can specify an arbitrary random visible universe by deciding what to put in each slot — one might leave a slot empty, put a proton or neutron in there, or perhaps stick in an electron or some other kind of particle.”

So, okay, I’m going to argue with that. But for now, let’s follow the flow of the Tegmark argument.

To keep things reasonably simple, let’s suppose we have ten alternate ways to fill each of the quintillion googol proton-sized slots. In that case, the number of possible ways to populate a home volume with matter consists of choosing among ten options a quintillion googol times in a row, which is ten to the quintillion googol power. In describing this number, it will be useful to use googol’s big brother, the googolplex, which is a number written as a one followed by a hundred zeroes. If googol is 10^100, then googolplex is 10^googol, or 10^(10^100).

10^(quintillion googol) = 10^(10^118) = 10^((10^100)x(10^18)) = (10^(10^100))^(10^18) = googolplex^quintillion

So now we know that there are at most googolplex-to-the-quintillion possible versions of how our visible universe could appear. A large number, yes, but if our universe is truly infinite, there will be an infinite number of possible home volumes besides ours, and it seems likely that one of them could be an exact match for your own. (Although, again, this is not a certainty.)

How far off might the first copy of our visible universe be? One idea might be to set out in a straight line and whip through the first googolplex-to-the-quintillion home volumes. Just for fun, let’s give this distance a made-up name: one striiide. Given that a home volume has a diameter of a octillion meters, a striiide is an octillion googolplex-to-the-quintillion meters. Would traveling this far guarantee a hit? Not quite.

A little calculating of probabilities indicates that if I travel one striiide, I have a 63% chance of encountering a home volume exactly like the one I started from (the precise probability is very close to 1 – 1/e, where e is the base of the natural logarithm). But as I travel more striiides, the odds go up, and after ten striiides, my chances of having found a visible universe exactly like ours is better than 99.99%.

So, the argument concludes, if the universe really is infinite, then there probably are other people exactly like us somewhere out there. I find this reductive and dispiriting—but I suppose someone might view it as liberating. Like, even if you goof up your life, some other you will get it right?

Nah, to hell with that. It’s like saying nothing I do in my life matters because one of these days I’ll be safe in heaven. Don’t bet on it!

In my next post, maybe next week, I’ll say more about how we might evade the dull Lego-block view of our world as being finite in the small. If it’s infinite in the large, why shouldn’t we be enjoying infinity right here and now. Right in our bodies, and in our minds!

Click for a larger version.

Your mind is an infinite Jackson Pollock. Stay tuned.

This entry was posted on Wednesday, May 27th, 2015 at 1:38 pm and is filed under Rudy's Blog. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.